DEFLEKSI DAN ROTASI BALOK TERLENTUR

Defleksi

Semua balok yang terbebani akan mengalami deformasi (perubahan bentuk) dan terdefleksi (atau melentur) dari kedudukannya. Dalam struktur bangunan, seperti: balok dan plat lantai tidak boleh  melentur terlalu berlebihan untuk mengurangi/meniadakan pengaruh psikologis (ketakutan) pemakainya.

gambar 1

Ada beberapa metode yang dapat dipergunakan untuk menyelesaikan persoalan persoalan defleksi  dan deformasi pada balok, diantaranya adalah: metode integrasi ganda (”doubel integrations”), luas bidang momen (”Momen Area Method”), dan metode luas bidang momen sebagai beban. Metode integrasi ganda sangat cocok dipergunakan untuk mengetahui defleksi sepanjang bentang sekaligus. Sedangkan metode luas bidang momen sangat cocok dipergunakan untuk mengetahui defleksi  dalam  satu  tempat  saja.

Asumsi yang dipergunakan untuk menyelesaiakan persoalan tersebut adalah hanyalah defleksi yang diakibatkan oleh gaya-gaya yang bekerja tegak-lurus terhadap sumbu balok, defleksi yang terjadi  relative kecil dibandingkan dengan panjang baloknya, dan irisan yang berbentuk bidang datar akan tetap berupa bidang datar walaupun terdeformasi.

\

1. Metode Integrasi Ganda

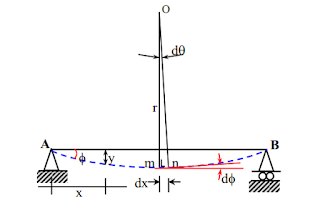
Suatu struktur  sedehana  yang  mengalami lentur dapat digambarkan sebagaimana, dimana y adalah defleksi pada jarak x, dengan x adalah jarak lendutan yang  ditinjau, dx adalah jarak mn, d sudut mon, dan r adalah jari-jari lengkung.

2. Metode Luas Bidang Momen

Pada pembahasan di atas telah dihasilkan lendutan yang berupa persamaan. Hasil tersebut masih  bersifat umum, namun mempunyai kelemahan apabila diterapkan pada 16 struktur dengan  pembebanan yang lebih kompleks, maka dirasa kurang praktis,  karena harus melalui penjabaran secara matematis.

Metode luas bidang momen inipun juga mempunyai kelemahan yang sama apabila dipakai pada  konstruksi dengan pembebanan yang lebih kompleks. Namun demikian metode ini sedikit lebih praktis, karena proses hitungan dilakukan tidak secara matematis tetapi bersifat numeris

3. Metode Luas Bidang Momen Sebagai Beban

Dua metoda yang sudah dibahas di atas mempunyai kelemehana yang sama, yaitu apabila  konstruksi dan pembebanan cukup kompleks. Metode ”Bidang Momen Sebagai Beban” ini pun dirasa lebih praktis dibanding dengan metode yang dibahas sebelumnya. Metode ini pada hakekatnya  berdasar  sama dengan metode luas bidang momen.

gamabr 2

hanya  sedikit  terdapat  perluasan.  Untuk  membahas  masalah  ini  kita  ambil  sebuah konstruksi seperti tergambar pada gambar, dengan beban titik P, kemudian momen dianggap sebagai beban

Deformasi

Deformasi (perubahan bentuk) balok disebabkan oleh beberapa faktor, diantaranya adalah  :  Akibat  beban  luar  yang  bekerja  (seperti  beban  merata,  terpusat,  segitiga,  dan sebagainya), momen pada salah satu ujung balok, dan perpindahan (translasi) relatif ujung balok terhadap ujung balok yang lain.

1.  Deformasi Akibat Beban Merata

Deformasi  yang  terjadi  pada  struktur  balok  yang  menahan  beban  merata sebagaimana digambarkan pada gambar,  dapat dihitung dengan metode luas bidang  momen sebagai beban.

2. Deformasi Akibat Momen Pada Salah Satu Ujung Balok 

Struktur balok yang menahan beban momen di ujung A sebagaimana digambarkan pada gambar. didapat bidang momennya berupa BMD. 

gambar 3

Balok sederhana yang menahan beban momen di Ujung A BMD  tersebut,  dipergunakan  sebagai  beban  sehingga  didapat  reaksi  perletakan.

3. Deformasi Akibat Beban Segitiga

Deformasi yang terjadi pada struktur balok yang menahan beban segitiga digambarkan  sebagaimana. Metode yang relatif lebih mudah adalah dengan metode integrasi ganda.

Share this post